Mountain building and an expanding Earth

In recent theories of an expanding Earth, it has been realized that if certain parameters apply, the building of mountain ranges is an inevitable consequence of expansion, and that the amount of uplift can be calculated, perhaps for the first time.

This article firstly examines the graphical and mathematical pictures involved, and secondly describes a simple experiment serving as the analogue of processes occurring in the Crust as expansion proceeds.

Graphical treatment

Fig. 1a. A smaller Earth of radius r with a crustal landmass ABCD resting on a parasolid mantle/core.

Figure 1a represents an arc AB of crustal material lying on the parasolid interior of a smaller Earth of radius r. The crustal material is assumed to consist of non-homogeneous solid materials, obeying normal physical laws, while underlying it is the mantle/core complex.

This mantle/core complex is treated as a parasolid, here implying that it behaves as an extremely viscous material which deforms very slowly under high pressure to maintain an essentially spherical shape. This deformation may occur by granular rearrangement or other route not typical of liquid flow.

In conventional Expanding-Earth theory, land areas have hung together with some retention of shape and orientation as the interior of the Earth has expanded under them, leaving formerly contiguous land areas separated by newly-formed rocks which mostly present as new seafloor.

The evidence suggests that the Earth has roughly doubled in radius over the last 200 million years (for more detail on this evidence, see my book Nuteeriat or the lead article Fixed-Earth versus Expanding-Earth Theories). This is an increase in radius of something around 3200 km, equal to about 1.6 cm per year.

Mountain ranges have a birth/death cycle time (from beginning of uplift to final planation) of around 10 million years. Over 10 million years, the increase in Earth’s radius will have been about 150 km.

To put some example values to Figure 1b, assume the land arc is 5000 km long, and its thickness is 30 km (this assumes a crust/mantle boundary, the Mohorovicic Discontinuity, at this depth. It also implies that this Discontinuity defines the boundary between normal solid and parasolid behaviour).

In Figure 1b the arc AB represents the lower surface of the land arc, in contact with the Discontinuity, and the arc CD represents the upper surface of the land, for simplicity assumed to be planar.

If the AB surface accommodates to the change in curvature of the parasolid base expanding under it, while the upper surface CD retained its original curvature above it, then CD would rise into a cylindrical dome above AB. Gravitational forces clearly make this impossible, and CD must collapse or crinkle on AB.

Graphical explanation

Fig. 1b. Geometry of a land arc on a smaller Earth

Figure 1b represents the land arc ABDC overlying a parasolid Earth sphere of radius r (not to scale). As the Earth parasolid component expands, the land arc will lie on a sphere of decreased curvature (Fig. 1c). This means that the CD surface of the arc becomes shorter while the AB surface slides on the parasolid sphere and remains of approximately constant length.

As a graphical image, this action can be taken to result in extrusion of a wedge of material at V.

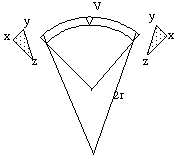
Fig. 1c. Change to a larger Earth, radius 2r, leads to excess material (xyz) at the upper surface of the land arc. This is equivalent in volume to the wedge of material at V.

If the material of the wedge reformed under gravity and pressure to form a mountain range, this range can be represented as the wedge V inverted on top of the land arc, as in Figure 1d. V represents a cross-section through the mountain range, lying at right angles to the plane of the figure.

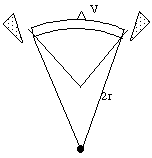
Fig. 1d. When recurved to a larger Earth of radius 2r, excess material shows up as a mountain range V.

The action results in a land arc with a mountain range superimposed upon it on a larger-radius Earth, as in Figure 1e.

Fig. 1e. Final conformation of the larger Earth of radius 2r, showing mountain formation by squeezing out a wedge of material through curvature decrease.

Mathematical explanation

Assume that the Earth’s radius 200 million years ago was r km, where r had a value of about 3185, corresponding to a circumference of about 20,000 km. Today’s radius is about 6370 km, or 2r. This is an average rate of radial expansion of about 1.6 cm/yr.

Referring to the land arc ABDC in Fig. 1a, at 200 million years ago (200 my) let us assume that AB had a length of 5000 km. If the segment was 30 km thick, the length of CD, the top of the arc segment, would be greater by about 47 km, using the usual circumference = 2¼r formula.

If we then do the calculations for a present-day Earth of radius 2r, with the land arc ABDC still 5000 km across but now sitting on the surface of a parasolid of lesser curvature (having expanded and reformed under the arc), the difference in length between AB and CD is now about 23.5 km.

In other words, if expansion had operated on the arc over the last 200 my solely to squeeze out a single triangular wedge of material to accommodate the decrease in curvature, that wedge would be 23.5 km wide and 30 km high. In practice, the accommodation would be expected to have occurred in a series of events, and in different places on the arc.

If we then assume each event of mountain uplift/erosion took 10 my, each event would produce a wedge of one-twentieth the cross-sectional area, say 10 km wide and 3.53 km high.

Clearly these are all highly simplified first-order calculations, but they do produce, perhaps for the first time, calculated results which are of the right order of magnitude. It should also be remembered that this mechanism is put forward as only one of the mechanisms which might lead to mountain building.

The foil experiment

A simple experiment was carried out using pieces of kitchen foil as an analogue of the processes suggested as occurring during Earth expansion.

Six pieces of aluminium foil each measuring 250 x 150 mm were cut from a roll of heavy-duty aluminium kitchen foil, and marked with a felt-tipped pen as in Figure 2.

Fig. 2. Marked sections of 150 x 200 mm kitchen foil.

Fig.3. Conical section of a horticultural ‘Gro-Tube’.



Fig.4. Conical section with 6 pieces of foil wrapped around it.

Fig. 5. The pack of 6 pieces of foil after flattening

Fig. 6. The lowest foil



Fig. 7. Foil one from bottom



Fig. 8. Foil two from bottom



Fig. 9. The foil two from top shows clear creasing



Fig. 10. Foil one from top



Fig. 11. The top foil shows a pattern of creases

While this simple experiment has obvious limitations -- for example, the crease positions were highly dependent on the directions used with the roller -- it does illustrate that the predicted surface creasing of upper layers does occur, as an analogue of mountain range formation on an Earth of decreasing surface curvature.