Jack Sprat Could Eat No Fat : Systel Allocation [MT107]
David Noel
<davidn@aoi.com.au>
Ben Franklin Centre for Theoretical Research
PO Box 27, Subiaco, WA 6008, Australia.

Jack Sprat could eat no Fat
..His Wife could eat no Lean
And so between the two of them
..They licked the platter clean
-- Old Nursery Rhyme
A Woman's Place is in the Home
There can be few phrases more likely to annoy 'the modern woman' than that just quoted,
and perhaps with reason. But before just dismissing it as a shining example of male
chauvinism, let us look at the situation, and others like it, from the viewpoint of Matrix
Thinking. At the same time we can try to work towards one of the general goals of this venture,
to develop more of the Unified Theory which can be applied to all systons.
In the present case, the syston involved is clearly that of the Family. The archetypical
family syston is made up of a Mother and a Father, often contracted together in an arrangement
called Marriage, and a number of Children. Of course there are often others involved, with
aunts, grandparents, and perhaps in-laws, but these are part of a wider syston called the
Extended Family. For the moment we are only concerned with a very simple unit, the basic
Family.
Working Together
In the nursery rhyme quoted at the head of this article, we have an example of successful
Systel Allocation -- the division of activities going on within a syston between the
components or elements of that syston, the systels.
That may be a fancy explanation for an obvious fact, but it it really so obvious? Do we
really take into account the real situation in a smooth-running syston, or do we tend to apply one of two extreme models to all systons? I suggest that the latter applies.
One extreme model is that of the 'Management Tree'. At the head of the Tree is the Boss.
Under the Boss work a number of subordinate or deputy bosses, and under them are people
occupying progressively more and more lowly positions until finally the lowest level of people
is reached, those who have no-one working under them.
This model is, even now, often still applied to the Family. On the Australian Census forms,
until recently there was a space to write in the name of the 'Head of Family' (now it says
'Person 1'). And, of course, in bigger and more complex systons, the Management Tree model
is the norm -- and there it is a quite reasonable model.
The other extreme is the 'Everybody's Equal' model. This is the model which is most often
applied to such things as electoral systems -- One Vote, One Value -- and there, again, it is
quite a reasonable model.
These are the extremes. In Matrix Thinking, it can perhaps be said that there are no
extremes, instead everything is a composite, a smear, across a spectrum where 'extremes' are
only arbitrary points towards the ends of the spectrums. We can take this reasoning further
to derive a useful result which cannot follow from any linear or highly-polarized view.
That result is the suggestion that any grouping in human society operates better, to produce
more 'well-being' among its members, if they work in a complementary fashion, with division
of tasks among them as well as between them.
Proposition 107A**. A syston improves its well-being when its components act
cooperatively and in complementary fashion rather than when all tasks are equally shared
This is perhaps not a very profound suggestion. But it is a fundamental one in what follows.
The Battle of the Sexes
The Battle of the Sexes has been perhaps the longest-running and most bloody of all the
battles in which human societies have engaged. This battle has been in a particularly active
condition for most of the Twentieth Century, with the early campaigns for Votes for Women,
the rise of Women's Lib in the 50's and 60's, and the subsequent adoption of Equal Pay for
women.
Nowadays I suspect most people would accept that the majority of these campaigns have
been won, by women, and we are left with tidying up the finer aspects of such things as Equal
Opportunity and Sexual Harassment legislation. Of course there will still be some women who
will cry "Not So!", and who will point to the "massive change in social attitudes which is still
needed before true equality can be gained".
Then, at a deeper level, there will be those who ponder whether it was all worth while,
whether the Victories Gained were Pyrrhic ones which really have not left women better off
in the long run. Whether the campaign to develop the New Male, sensitive, caring, and
communicative, sharing equally in everything that goes on, is really the ultimate battle.
Whether when this ultimate battle is won, women everywhere will henceforth be happy,
relaxed, and contented with the world.
Fig. 107.1. The Battle of the Sexes
It seems to me that there are two distinct aspects to the matter. One is the aspect of Equality
of Opportunity; the other is that of Division of Labour. Let us now go into this a little more
deeply.
Equality of Opportunity
Here is an area where Matrix Thinking will not lead to a view which diverges very much
at all from that commonly accepted. On a broad view, any artificial restriction on the actions
of particular people or systels (triggered solely by one of their characteristics) will reduce
infocap flow and hence synenergy. Thus if the aim is to maximize synenergy in their wider
syston, such restrictions are undesirable.
If the characteristic involved in itself places a limitation on the action, then that's life, and
the restriction involved is not artificial. There is a basic physical characteristic which hinders
men from giving birth, so they are not being denied anything in this. If women are denied the
opportunity to enlist for active service in an army, where they may be put in a situation of
needing to kill other soldiers, then that is artificial, and on a preliminary view, at least, such
a restriction is undesirable.
Then there is the topic of restrictions which go the other way -- Affirmative Action, quotas
for different ethnic groups in employment, special laws for aborigines and the like. The MT
approach just says the same thing: if the broad aim is to improve the wider syston, these
restrictions too must be undesirable
Division of Labour
This heading is used here to include much more than its application in industry. It is
broadened to include the activity of systels in any segment of the Matrix. We can look, for
example, at the situations under which plants grow.
In his book The Botanic Man, David Bellamy [Reference 4] looks at how different plant ecologies
have developed in different areas, according to the local average temperatures and rainfalls (or
more strictly, precipitation, including snow). He presents a picture along the lines of Figure
107.2.
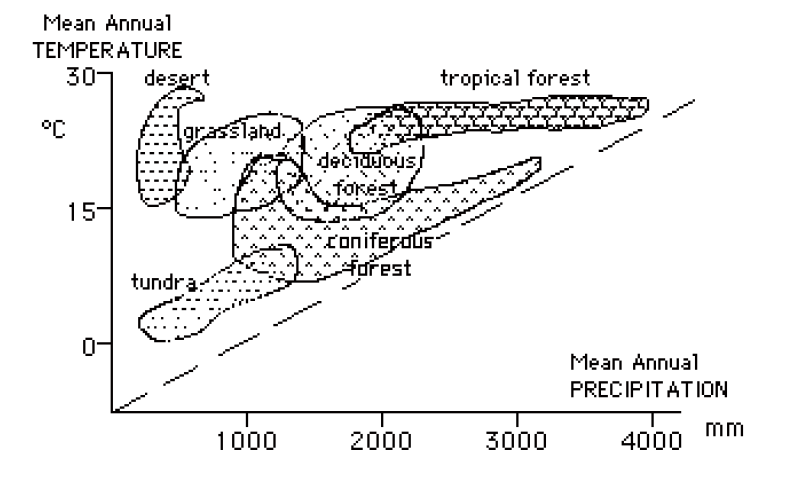
Figure 107.2. Vegetation and climates
Of course a picture like this is useful for working out what types of vegetation can be
expected under given temperature and rainfall conditions. But it has been included here for
another purpose.
The picture itself can be regarded as one particular cross-section across one segment of the
World Matrix. In MT108 we will be developing the idea of the Matrix Cocoon and
sections across it, but for the moment we can just regard the picture as a slice of the real world.
The illustrative value of this picture lies in the fact that it demonstrates very graphically
how systons can evolve to fill as much as possible of the 'Matrix Space' available. Only the
area above the dashed line represents conditions found in practice -- there are no very cold
regions with 3 metres or more of precipitation, for example.
Of course each of the vegetation types shown in Figure 107.2 is itself a generalization over
a large range of separate ecologies. Pictures similar to the above can be built up for subecologies
within one of the above types, such as that within a tropical forest.
In such a section across tropical forest 'Matrix Space', the axes of the picture might be such
things as height above ground and light incidence needed. For example, some groups of plants
are both tiny and require relatively little light. These can survive on the ground beneath a
continous tree canopy. Others are light-demanders and strive to grow into big trees; these must
either wait, scarcely growing, until a break in the canopy occurs through an ancient tree
crashing to the ground, or must possess a seeding mechanism which is rapidly triggered by the
occurrence of such a break.
Tropical forest ecologies are notable for their complexity and diversity. Their constituents
have evolved to fill every scrap of the available ecological space. For this reason it is completely understandable that their productivity is the highest of all ecological classes, 20
or 50 times that of semiarid savannahs or grasslands. The productivity is a reflection of the
diversity, as would be expected in MT terms.
Stability Through Diversity
There is also another, perhaps generally unappreciated, advantage to complexity. More
complex systems (those with higher infocap content) are found, in practice, to be more stable
than simpler ones. They can withstand changes and unexpected extremes of external
conditions far better than their simpler analogues. This is also true of human-based systons.
Proposition 107B**. Complex systons have greater stability than simpler ones
At first sight this might seem to be an unlikely rule -- it might be thought that the more
complex a system is, the more likely it is to go wrong. But in practice, examples can be found
at every level -- from computer programs through tribal conflicts and on to large modern
nations -- which bear out the validity of this Proposition.
In MT terms, what we are saying is that infocap and synenergy are what glues the parts of
a syston together, so that up to a point, the more glue, the better it will hold together. Of course
this concept breaks down when there is more glue than parts to glue together -- perhaps an
expression of "more money than sense", or "ruined by a lottery win"?
Yin and Yang
The general MT conclusion so far is that the greater the number of elements in a system,
and the more they work together, the better for the whole -- synenergy advantages systons.
But there is an observation on real systons which does not affect this conclusion, but adds
another consideration to it.
So far we have not looked at the mix of individual systels within a syston to any extent,
other than to note that their diversity is an advantage. Another aspect is their 'pecking order',
whether some of them come to dominate others, and in turn be dominated by others still. Every
human organization has some sort of dominance structure of this type, whether defined or
unwritten, every real syston has some element of the 'Management Tree' structure mentioned
at the beginning of this article.
The interesting thing is, when you look at it closely, that the majority of successful systons
seem to have two systels, not one, at the top. Typically, one of these dominators is effectively
'in charge' for many syston functions, while the other can step in and make a go of it when the
first is absent. And the other dominator is in charge for other functions, backed up by the first
when necessary.
The most obvious example is the Family. Typically, it consist of the Mother, the Father,
and a number of children. Again, typically the Mother is the dominator in home matters, the
Father dominates in extracting infocap from outside the syston. There is nothing necessarily
so in this, and of course role reversal is quite possible, but that is the common situation.
In politics, the general situation in a democracy of any nature is to have two major political parties, two dominators, and an unspecified number of minor parties. Occasionally one of the
minor players may rise in dominance and displace one of the two leaders, but the situation soon
settles down to the typical two dominators again. A problem with some electoral systems is
that they can fragment representation so much that it is difficult for the two dominators to
'coalesce' out of the Matrix swirl.
In business and social organizations, it is typical to have a Head and a Deputy. In active
systons, the role of the Deputy may actually be formally defined to include oversight of
particular functions in the normal run, with the switch-role of standing in for the Head where
necessary.
In physiological functions, most creatures have function operators in pairs. We have two
hands, left and right, of which one usually dominates. We have two ears, and two eyes. Some
spiders have eight eyes, and the primitive New Zealand reptile the Tuatara has the vestiges of
a third eye. Why have we settled on two?
Two Heads are Better than One
And, in effect, we have two brains, the left and the right hemispheres. We now know that
most human brain processes are allocated between these two, we know the sites of imagination,
of logical reasoning, of speech, of hearing, of motor functions. And we know from experience
with brain-damaged stroke victims that if one of these sites is damaged, others will attempt to
stand in and compensate.
We have already looked at the Battle of the Sexes, and pointed out some situations where
the naturally evolved order is for one sex to dominate in some areas, the second in others. Of
course there are many primitive organisms which do not have differentiated sexes, but instead
reproduce by budding. The history of evolution of higher plants and animals is the history of
increasing diversity and complexity in sexual matters.
Thus in the most evolved plants, the angiosperms like the oaks and the grasses which are
all around us, each female 'egg' cell in the flower requires fertilization by two male cells
derived from pollen. In the more primitive plants, the gymnosperms like the pines and cycads,
only one male cell is needed. The first group has its egg cells within a special structure, the
ovary, which the gymnosperms lack -- the name gymnosperm actually means 'naked seed'.
To sum up, the theme of the present article is to bring out the ideas that diversity benefits
a syston, that allocation of complementary roles within a syston rather than multiplying
standard roles also benefits a syston, and finally that for particular functions of the syston it
works out best if two systels come to dominate that function, with one backing up the other.
Proposition 107C*. The optimum number of dominant systels in a syston is two
To give some perspective to these ideas, it should be noted that they are not theoretically
derived. Instead, they are the result of analyzing actual situations, and noting aspects which
have generally ended up on top in the Survival of the Fittest.
We can move on (MT108) now to look at another aspect of systons -- how all their components
interact together, and what rules they follow in these interactions.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

References
(Full list of references at MTRefs)
[4]. David Bellamy. Botanic Man. Hamlyn, London, 1978.
Go to the "Matrix Thinking: How Society Works" Home Page
Versions 1.0-1.2, printed editions (Matrix Thinking Book I, BFC Press, Australia, 1992-1997)
Version 2.0, 2004, PDFs etc on World Wide Web (http://www.aoi.com.au/matrix/MT.htm)
Version 3.0, 2014 Jul 6-23, Reworked from chapter 121 of "Matrix Thinking" as one article in a suite on the World Wide Web.




